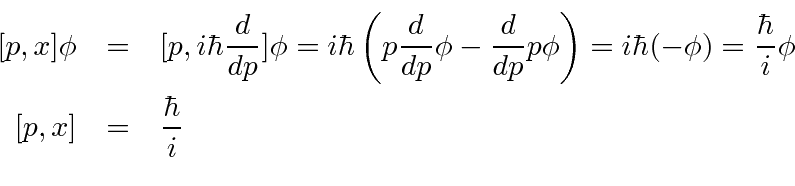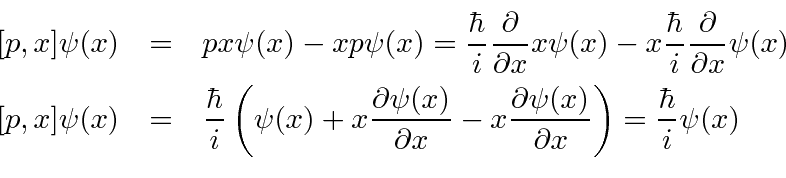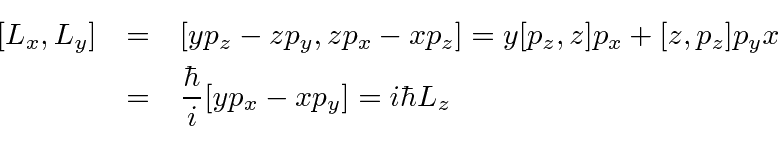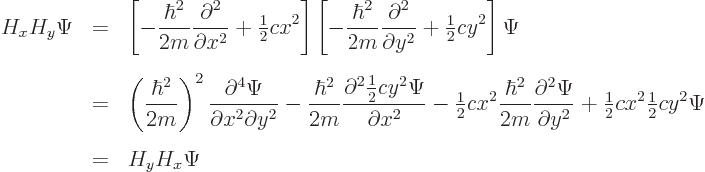Commutators
11.2: Operator Algebra - Chemistry LibreTexts
![SOLVED: As was proven in class, the basic commutation relation between the position and momentum operators is [x,p] = Use this and the operator identity for commutators of product operators (also proven](https://cdn.numerade.com/ask_images/1ebcef2e9ae049358ffcc28486d9aef0.jpg "SOLVED: As was proven in class, the basic commutation relation between the position and momentum operators is [x,p] = Use this and the operator identity for commutators of product operators (also proven")
SOLVED: As was proven in class, the basic commutation relation between the position and momentum operators is [x,p] = Use this and the operator identity for commutators of product operators (also proven
Commutator: linear momentum and position - YouTube
SOLVED: As we have discussed the lowering and raising operators are defined by W1/2 2h a uwh where i = y–1, and w is a real number. Taking into account the fundamental
![PDF] Generalized geometric commutator theory and quantum geometric bracket and its uses | Semantic Scholar](https://d3i71xaburhd42.cloudfront.net/90e6f2f3638caf68d5e689dafe958c5025edb8d6/9-Table2-1.png "PDF] Generalized geometric commutator theory and quantum geometric bracket and its uses | Semantic Scholar")
PDF] Generalized geometric commutator theory and quantum geometric bracket and its uses | Semantic Scholar
![Quantum Mechanics: Commutators] The answer is 2[d/dx] but I keep getting [d/dx], where is the 2 coming from? : r/HomeworkHelp](https://preview.redd.it/otcvhbhs3ys31.png?auto=webp&s=ada2c6ab39a10df19261341308d26ea64c248714 "Quantum Mechanics: Commutators] The answer is 2[d/dx] but I keep getting [d/dx], where is the 2 coming from? : r/HomeworkHelp")
Quantum Mechanics: Commutators] The answer is 2[d/dx] but I keep getting [d/dx], where is the 2 coming from? : r/HomeworkHelp
Commutators
Fundamental Commutation Relations in Quantum Mechanics - Wolfram Demonstrations Project
Topics Today Operators Commutators Operators and Commutators - ppt download
PDF) BIRTH OF THE COMMUTATION RELATION IN QUANTUM MECHANICS
QUANTUM MECHANICS Homework set #5: Commutators ...
Challenging commutator algebra problem in quantum mechanics | Physics Forums
Quantum Mechanics_L3: Some commutation relations - YouTube
Quantum Mechanics/Operators and Commutators - Wikibooks, open books for an open world
XV Angular momentum‣ Quantum Mechanics — Lecture notes for PHYS223
Quantum Mechanics/Operators and Commutators - Wikibooks, open books for an open world
Unacademy - India's largest learning platform
The Commutators of the Angular Momentum Operators
MathType on Twitter: "In #Quantum #Mechanics we can use the #commutator of two operators to know if the observables associated to those operators are compatible, in which case we can find a
4.5 The Commutator
How to use sympy.physics.quantum Operator? - Stack Overflow
quantum mechanics - Spatial Translation Commutation with Position Operator in QM - Physics Stack Exchange
![تويتر \ Tamás Görbe على تويتر: "Commutation relations like this form the basis of quantum mechanics. This example expresses the connection between position (X) and momentum (P): [X,P]=XP-PX=ih/2π, where h is Planck's](https://pbs.twimg.com/media/E_o9UrsXsAQCKX1.png:large "تويتر \ Tamás Görbe على تويتر: \"Commutation relations like this form the basis of quantum mechanics. This example expresses the connection between position (X) and momentum (P): [X,P]=XP-PX=ih/2π, where h is Planck's")
تويتر \ Tamás Görbe على تويتر: "Commutation relations like this form the basis of quantum mechanics. This example expresses the connection between position (X) and momentum (P): [X,P]=XP-PX=ih/2π, where h is Planck's
